1.2 概率论

Posted on by Dennis

02c41bc6b30ba13e82b8cd7a8f8fd844.png
65915983c89fde987179accb402a51cc.png

1.2.3 贝叶斯概率

1.1 例子：多项式拟合中贝叶斯公式:结合观察数据提供的信息,将先验概率转化为后验概率
以多项式拟合为例:

  1. 在观察数据之前,我们做出先验分布假设 P(W), (实际上就是选择什么模型)
  2. 观察数据 D={t_1, t_2,...t_N}的影响,利用条件概率P(D|W)表示,条件概率表示对数据集进行评估,表征数据集在不同w在数据集 D 下的可能性(这里的似然概率不是一个在 w 上面的概率分布,因此概率和不等于1)
  3. 根据先验概率和似然函数计算后验概率,用P(w|D)=\frac{P(D|W)\cdot P(W)}{P(D)}来表示, P
    贝叶斯定理的定义
    posterior \propto likelihood \times prior
    所有变量都可以视作是 w 的函数, 分母的目的是归一化, 确保后验分布是和为1的概率密度分布.我们用似然函数来表达先验概率:
    p(D)=\int p(D|w)p(W)dw
  4. 似然函数在频率学派中:
    w 被视为客观存在的参数,参数的值有某种形式的"估计器"确定, w通过考虑数据集 D 的所有可能的分布来估计.

    • 常用的估计器为极大似然.在机器学习文献中，似然函数的负对数是误差函数中的一种,因为负对数是单调递减函数，所以最大化可能性等同于最小化误差.

    • 另一种估计器为 bootstrap:假设数据集有 N 个点构成X={x_1,...,x_N}.从X中随机抽样 N 个点构建新的数据集X_B并进行替换,一些 X 中的点可能被X_B中的点替换,而 X 中的其他店可能不在X_B中.如此往复 L 次从由 N 个点构成的原始数据集X 中生成 L 个数目数据集.然后可以通过观测模型在不同数据集之间的预测的变动来评估参数估计的统计准确度

  5. 似然函数在贝叶斯学派中:
    只有一个数据集 D(实际观察到的数据集),参数的不确定性通过 w 的概率分布来表示. 这对应于选择w的值，其中观察到的数据集的概率被最大化。
    优点:先验知识自然而然产生.
    缺点:

    • 先验的选择是基于数学上的方便选择的(共轭先验),而不是任何先验知识.
    • 先验知识的选择也很困难.
    • 先验模型的错误选择对于结果的影响很大
      频率学派的一些评估方法为以上问题提供了解决方法,例如交叉验证等.

例子:抛三次硬币都是正面,对于频率学派来说,似然估计概率正面为1.对于贝叶斯学派,不会给出那么极端的结果.

1.2.4 高斯分布

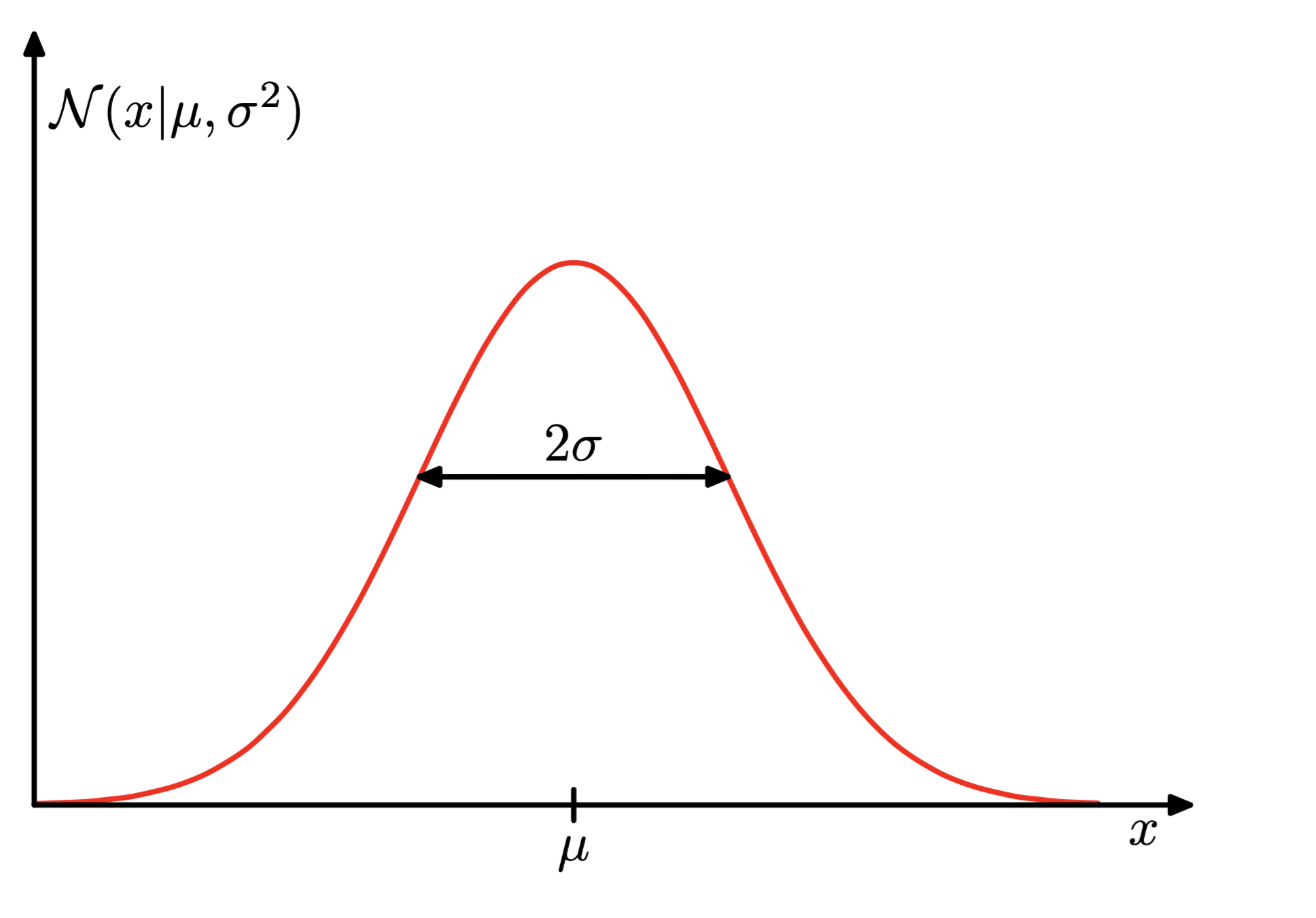
高斯分布定义:
\mathcal{N}(X|\mathcal{u},\sigma^2) = \frac{1}{(2\pi\sigma^2)^{\frac12}}\exp{-\frac{1}{2\sigma^2}(x-\mathcal{u})^2)}
\mathcal{u}被称为均值,\sigma^2被称为方差,\sigma标准差,方差的倒数\beta=\frac{1}{\sigma^2}称为精度.
高斯分布的性质:
\mathcal{N}(x|\mathcal{u}, \sigma^2)>0
\int_{\infty}^{\infty}\mathcal{N}(x|\mathcal{u},\sigma^2)dx=1
2eb1d44d36549a8333336650cc308e7d.png
x 的平均值为
\mathbb{E}[x]=\int_{\infty}^{\infty}\mathcal{N}(x|\mathcal{u},\sigma^2)xdx=\mathcal{u}
对于二阶矩
\mathbb{E}[x^2]\int_{\infty}^{\infty}\mathcal{N}(x|\mathcal{u},\sigma^2)xdx=\mathcal{u^2} + \mathcal{\sigma^2}
正态分布的方差为
var[x]=\mathbb{E}[x^2]-\mathbb{E}[x]^2=\sigma^2
连续变量的D维度下的高斯分布公式:

\mathcal{N}(x|\mathcal{u},\Sigma) = \frac{1}{(2\pi)^{\frac{D}{2}}} \frac{1}{|\Sigma|^{\frac12}}\exp{{-\frac12(x-\mathcal{u})^T\Sigma^{-1}(x-\mathcal{u})}}
其中\mathcal{u}是 D 维,且D \times D的矩阵\Sigma是协方差矩阵,|\Sigma|是协方差矩阵的行列式.
faf009c1e95036fa8361d3943ee9841b.png
如何理解似然函数:正态分布的似然函数为例,通过不断调整均值和方差使得似然函数能够完美拟合所有数据集.
我们可以把每个样本看成是一个事件,我们认为样本之间服从独立同分布(i.i.d.),两个独立事件的联合概率由每个时间的边际概率的乘积给出.我们可以计算出整个数据集的概率:
p(x |\mathcal{u}, \sigma^2)=\prod_{n=1}^N \mathcal{N}(x_n|\mathcal{u},\sigma^2)
极大似然估计就是找到使似然函数最大化的参数值,在实际处理中,最大化极大似然函数的对数更加方便(因为对数函数是增函数,所以优化函数的对数等价于直接优化函数),此外大量小概率乘积会降低计算机计算精度.
对数似然概率函数被写作
\ln p(x|\mathcal{u},\sigma^2) = - \frac{1}{2\sigma^2}\sum^N_{n=1}(x_n -\mathcal{u})^2 - \frac N2 \ln \sigma^2 - \frac N2 \ln (2 \pi)
对于\mathcal{u}的最大化,我们可以得到
\mathcal{u}_{ML} = \frac{1}{N} \sum^N_{n=1}x_n
\sigma_{ML}^2 = \frac{1}{N} \sum^N_{n=1}(x_n-\mathcal{u})^2
极大似然估计法的不足:低估了分布的方差
统计学上面解释过偏差(有偏估计和无偏估计):
我们认为,u_{ML}和\sigma^2_{ML}是有限个数据集 X 上的极大似然估计参数,我们认为这些数据集本身是从一个具有服从\mathcal{u}和\sigma^2高斯分布的超数据集从抽样而来,直观的说:
\mathbb{E}[u_{ML}] = u
\mathbb{E}[\sigma^2_{ML}] = (\frac{N-1}{N})\sigma^2
我们会获得正确的均值,但是会获得会低估真实的方差,具体怎么低估的参考10.1.3
2d9d5db80ec8ba866d51566ffc832648.png
随着数据点数N的增加，最大似然解的偏差变得不那么显着，并且在极限N\rightarrow \infty中，方差的最大似然解等于生成数据的分布的真实方差。在实际中,这个偏差不是一个大问题.但是在某些更负责的模型中,最大似然相关的偏差问题会更加严重.从统计学角度看,过拟合问题的根源就在于极大似然估计的偏差.

1.2.5 再探曲线拟合

从概率论的角度看曲线拟合,误差函数, 正则化.对于函数拟合问题,我们使用概率分布表达对目标标签的不确定性. 对此我们假设标签服从高斯分布, 标签的均值由多项式拟合中训练出来的y(x,w)决定, 因此我们有:
p(t|x,w,\beta) = \mathcal{N}(t|y(x,w),\beta^{-1})
272e389d8896e77a3c85a6a713458d9f.png
我们现在使用极大似然估计,利用训练数据{x,t}来估计w和\beta, 我们假设数据间满足独立同分布.则似然函数给出为:
p(t|x,w,\beta) = -\frac{\beta}2 + \sum_{n=1}^{N}{y(x_n, w)-t_n }^2 + \frac N2 \ln \beta - \frac{N}2 \ln(2 \pi)
极大似然解用w_{ML}表示, 实际优化的过程中,做出的处理有:

  1. 忽略掉最后两项\sum_{n=1}^{N}{y(x_n, w)-t_n }^2 和 \frac N2 \ln \beta - \frac{N}2 \ln(2 \pi)
  2. 正常稀疏缩放不会影响最大值,因而把前面\beta / 2替换为1 / 2
  3. 优化负的对数自然,而不是最大化对数自然
    因此，在高斯噪声分布的假设下最大化似然性的结果出现了平方和误差函数.
    我们可以利用极大似然估计确定在条件高斯分布下参数\beta, 优化似然函数我们可以得出:
    \frac{1}{\beta_{ML}} = \frac1N \sum_{n=1}^N {y(x_n, w_{ML}) - t_n}^2
    确定了参数w和β后，我们现在可以对未知量 x 进行预测.建立似然概率预测模型:
    p(t|x,w_{ML},\beta_{ML}) = \mathcal{N}(t|y(x, w_{ML}), \beta_{ML}^{-1})
    现在我们更进一步,在多项式系数 w 上面引入先验概率, 在此之前,我们先考虑高斯分布的另一种形式:
    p(w|a) = \mathcal{N} (w|0,a^{-1}\mathbb{I})=(\frac{a}{2\pi})^{(M+1)/2} \exp {-\frac{\alpha}{2}w^Tw}
    其中\alpha为分布的精度,M+1是 M 阶多项式参数向量 w 的元素个数.控制模型精度变量alpha被称为模型的超参数,我们得到如下后验概率:
    p(w|x,t,\alpha,\beta) \propto p(t|x,w,\beta)p(w|a)
    我们现在可以通过最大后验概率来使得 w 最大化, 这个技术被称为 MAP.取 p(w|a)的负对数并与后验概率计算公式,似然函数计算公式结合我们可以得到,最大化后验概率等价于最小化:
    \frac{\beta}2\sum_{n=1}^N {y(x_n, w) - t_n}^2 + \frac{\alpha}2 w^Tw
    正则化从从某种意义上来说就是先验分布,\lambda = \alpha / \beta

贝叶斯曲线拟合

上面我们只是使用了点估计,在完全贝叶斯方法中，我们应该始终如一地应用概率的和和乘积规则，正如我们将要看到的那样，我们需要整合w的所有值。这种方法是贝叶斯模式识别方法的核心
在预测问题中,给定训练数据 x_{train}, 测试数据 x_{test}, 和标签 t 我们需要评估预测分布p(t|x_{train},x_{test},t)对于完全贝叶斯来说,这种预测分布表达如下:
p(t|x_{train},x_{test},t) = \int p(t|x_{train},w)p(w|x_{test},t)dw

这里的公式怎么来的?
4b8ecc1998b2bee0b8a2602e10b236a3.png

其中p(t|x_{train},w)由1.2.4中的公式
p(t|x,w,\beta) = \mathcal{N}(t|y(x,w),\beta^{-1})
p(w|x_{test},t)是后验分布,3.3节中我们可以看到,对于曲线拟合问题后验分布是高斯分布且能够精确拟合.最后预测分布的形式也由高斯分布给出
p(t|x_{train}, x_{test}, t) = \mathcal{N}(t|m(x),s^2(x))
其中均值为
m(x) = \beta \phi(x)^TS\sum_{n=1}^N \phi(x_n)t_n
方差为
s^2(x) = \beta^{-1} + \phi(x)^TS\phi(x)
其中\beta^{-1}表示由于噪声引起 t 预测值的不确定性,这种不稳定性实际上是前一节中的\beta_{ML}^{-1},第二项为参数 w 的不确定性,矩阵 S 为:
S^{-1}=a\mathbb{I} + \beta \sum_{n=1}^N \phi(x_n)\phi(x)^T
其中\mathbb{I}为单位矩阵, 向量\phi(x)是参数,\phi_i(x)=x^i其中i=0,...,M
58141fa95c543de3e093e704434bdd6b.png

发表回复

您的电子邮箱地址不会被公开。