1.5 决策理论

1.5决策问题

我们在1.2节中看到概率论如何为我们提供量化和操纵不确定性的一致数学框架，在这节，我们转向对决策问题的讨论，当决策问题与概率论结合时，我们能够在涉及不确定性的情况下做出最优决策，例如在模式识别中遇到的那些问题。
假设我们有一个输入向量x和属于向量的标签t，我们的目标是预测给定未知量 x 情况下，给出预测的标签t。对于回归问题，t将包括连续变量；而对于分类问题，t将表示类别标签。联合概率分布p(x,t)为不确定下的参数估计提供一种可行的方法。从训练数据中确定p(x,t)是一个inference的例子，这通常是一个非常困难的问题，其解决方案构成了本书大部分内容的主题。然而，在实际应用中，我们必须经常对t的值进行具体的预测，或者更一般地根据我们不同预测的值采取不同的行动，这个方面是决策问题的主题.例如，考虑一个医疗诊断问题，我们已经拍摄了患者的X射线图像，我们希望确定患者是否患有癌症.在这种情况下，输入向量x是图像中像素的集合，输出变量t将表示癌症的存在，我们用C1类表示，或者没有癌症，我们用C2类表示有癌症.我们可以选择t为二进制变量，使得t=0对应于C1类，t=1对应于C2类.稍后我们将看到，标签值的类型对于概率模型的选择来说特别方便.那么推理问题涉及确定联合分布,这里给出完整的概率概率描述p(x,Ck​)(或者写p(x,t)).这是决策步骤，决策问题告诉我们如何在适当的概率下做出最优决策.我们将看到，一旦我们解决了推理问题，决策阶段通常非常简单.如下介绍决策问题的部分思想:
在进行更详细的分析之前，让我们首先考虑期望概率如何在决策中发挥作用.当我们为新患者获得X射线图像x后，我们的目标是决定分配一个标签给新图像.我们需要的是新患者 x 在两个类的概率,他们由条件概率p(Ck​∣x)确定.基于贝叶斯定理,这些概率可以表述为:

p(Ck​∣x)=p(x)p(x∣Ck​)p(Ck​)​

边缘分布可以经由条件概率或累加获得, 我们可以把 p(C_k)理解为类别Ck​的先验概率,p(Ck​∣x)为后验概率.p(C1​)表示在 X 射线测量之前,一个人患有癌症的概率, 类似地,p(C1​∣x)是根据 X 包含的信息使用贝叶斯定理对先验概率进行修正.如果我们的目标是最小化将x诊断为错误类型的概率，那么直观地我们会选择具有更高后验概率的类.

1.5.1 最小化错误分类的概率

假设我们的目标只是尽可能减少错误分类, 我们需要一个规则把x划分为不同的标签.这个规则将输入空间划分为不同的区域Rk​ ,我们将其称为决策区域.对于决策区域Rk​中的所有点, 我们将其划分到类别Ck​.

决策区域之间的边界称为决策边界或决策表面, 注意，每个决策区域不需要是连续的，而是可以包括一些不相交的区域. 为了找到最优决策规则，首先考虑如癌症问题两个类的情况，当属于类C1​的输入向量被分配给类C2​时，会发生错误，反之亦然.分类错误的概率为:

p(mistake)=p(x∈R1​,C2​)+p(x∈R,C1​)

=∫R1​​p(x,C2​)dx+∫R2​p(x,C1​)dx

在目前,我们可以任意选的分类规则将每个点分配到不同的类.为了最小化误差,我们应该将 x 划分到积分最小的类(也就是说,划分到正确的类),对于给定的 x 值,若p(x,C1​)>p(x,C2​)那么我们应该将 x 的标签分配给C1​类,根据概率的乘积规则,我们有p(x,Ck​)=p(Ck​∣x)p(x)由于p(x)是公共项,因而我们等价于最小化,如果把 x 分配给后验概率p(Ck​∣x)最大对应的类中,划分错误的概率.

针对 x 绘制的两个类中每一个类在决策边界x=x^下的联合分布p(x,Ck​)示意图, 对于任意x<x^数据决策区域R1​ 内的点,我们将其分类为C1​, 其中误差来源于绿色,红色,蓝色的区域,对于其中x<x^ 误差来源于错误地将原本属于C2​类的点划分为C1​, 对应于(红色和绿色的面积和来表示);相反对于区域x≥x^的点,误差来源于错误地将划分为C2​的点划分为C1​(对应于蓝色区域).当我们改变决策边界的位置x^时,蓝色和绿色对应的面积大小保持不变,但是红色区域的面积发生变化.决策边界b^的最佳选择是p(x,C1​)和p(x,C2​)之间曲线交叉的交点对应的 x,在这种情况下,红色的区域消失.这等价于最小错误率的决策规则,它将 x 的每个值分配给具有较大后验概率p(Ck​∣x)对应的类.

对于 K 个分类情况,最大化正确划分的概率稍微容易一些:

p(correct)=k=1∑N​p(x∈Rk​,Ck​)

=k=1∑K​∫Rk​​p(x,Ck​)dx

当决策区域R最大化,使得每一个 x 被分配到p(x,Ck​)对应的最大的类,我们同样使用乘法规则p(x,Ck​)=p(Ck​∣x)p(x), 值得一提的是,由于p(x)是公共项, 所以我们等价于最大化后验概率 p(Ck​∣x)

最小化期望误差

我们的目标将会比简单地减少错误分类的样本数要更加复杂,我们继续考虑医学诊断的问题,如果没有癌症的患者被诊断为患有癌症,那么该患者可能需要进一步检查. 相反如果一个患有癌症的患者被误诊为健康,那么结果是由于缺乏治疗而过早死亡.因此,这两种错误引发的后果可能大不相同.显然,即使回造成更多的第一类错误,但是显然减少第二类错会更好.
对于这类问题,我们可以引入损失函数来解决这些问题,这是思路是统一解决所以分类问题想法.我们的目标是尽量减少总损失.假设对于一个未知的样本x,它的标签是Ck​, 我们的模型把Ck​分类为Cj​(这里 j 是否等于 k 不一定), 在分类的过程中,一定会产生一定程度的损失,我们用Lkj​表示.如果都做出了正确的分类,那么不会发生损失,如果健康的患者被诊断为患癌症, 那么就会产生1个 loss, 但是如果一个患有癌症的患者被诊断为健康, 那么损失就是1000个 loss.

一个矩阵损失的例子, 其中其中包含Lkj​癌症治疗问题,行对应了真正问题的类,列对应了我们我们做分类时候的预测结果
最佳方案是最小化 loss, 然而损失函数取决于真正的标签,但是这个标签是未知的.对于给定的输入向量 x, 在真实分类标签的不确定性通过联合概率分布p(x,CK​)来表示, 我们寻求最小化平均损失,这个损失的平均值是相对于联合概率分布计算的

E[L]=k∑​j∑​∫Rj​​Lkj​p(x,Ck​)dx

这里是 k 个真实分类,j 个决策区域

每一个输入向量 x, 可以独立被分配到决策区域Rj​.我们的目标是选择一个能够最小化误差的决策区域Rj​,也就是每一个样本应该最小化∑k​Lkj​p(x,Ck​),和上文一样,我们可以使用乘积规则来消除p(x)的公共因子.因而损失函数被为一个样本被划分到每一个类中的效用期望和:

k∑​Lkj​p(Ck​∣x)

一旦我们知道后验概率p(Ck​∣x)问题就得到解决.

1.5.3 拒绝域

拒绝选项的例子,输入 x 使得两个后验概率中小于或等于某个阈值的θ将会被拒绝
设置一个阈值,当最大后验概率大于某个阈值时候,我们把它划分为1类,反之划分为2类.如果θ设置为1,那么将会明确拒绝所有样本,如果划分为 k 类,那么设置θ<1/k表示为接受所有示例.

1.5.4 推断&决策

推断:使用训练数据学习一个模型,获得p(Ck​∣x)
决策:利用这些后就概率进行最优分类
另一种想法是将这两个问题一起解决, 简单的学习一个关于 x 的分类函数.有三种具体的方法:一下根据模型复杂度由杂到简为:

1. 各自解决每个类Ck​的问题,分别求出p(x∣CK​).各自求出每个先验概率p(Ck​),然后利用贝叶斯公式

p(Ck​∣x)=p(x)p(x∣Ck​)p(Ck​)​

其中对于先验概率p(x)我们有:

p(x)=k∑​p(x∣Ck​)p(Ck​)

等价于我们可以直接对联合分布p(x,ck​)进行建模, 然后归一化获得后验概率.找到后验概率后,我们可以为位置样本 x 划分分类. 隐式或显式地对输入和输出的分布进行建模被称为生成模型.因为他们通过采样,可以在输入空间中生成合成数据点.

2. 解决后验概率p(Ck​,x)模型的建立,然后使用决策模型为位置样本划分为一个新类.这种直对后验概率进行建模的方法被称为判别模型.
3. 找到一个函数f(x),称为判别函数,直接实现对标签的映射,对于二分类问题f(x)的输出是一个二进制, 在这种情况下概率论不起作用.

方法评价:

1. 方法(a)是最严苛的,因为需要在x和Ck​上面寻找联合分布. 在许多场合下,x 的维度较高,我们需要更大的训练集以便得到较高的算法性能.类先验概率p(Ck​)通过训练集的样本标签分布中估算出来.对于异常值检测(有些标签概率比较低)方法 a 比较适合.
2. 找到联合分布p(x,Ck​)实际上只需要通过找到后验概率p(​Ck​,x)获得可以直接使用方法( b )得到,实际上有很多种对后验概率影响不大的类条件密度
   

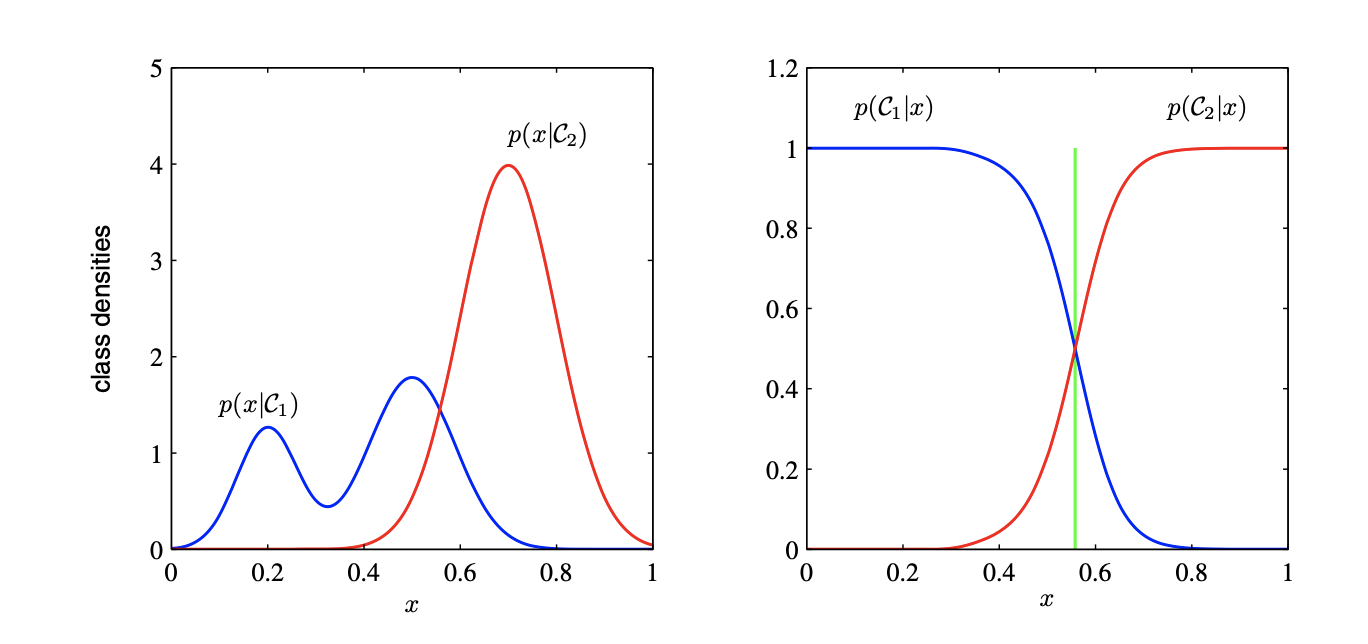
如图是在只有一个输入变量 x(左图)的两个标签类的条件密度及相应的后验概率示意图.左侧图中蓝色线是条件密度p(x∣C1​), 这个条件密度对后验概率没有影响,右图垂直绿色表示 x 的决策边界,它给出了最小错误分类概率.

3. 方法 C 比较简单,我们利用训练数据来找到将每个x直接映射到类标签上的判别函数f（x），从而将推理和决策阶段组合成统一的学习问题.在图中，最小概率的决策边界对应于图中的绿色线,但是使用方法 C 我们就不能计算出后验概率p(Ck​∣x), 但是计算出后验概率是很有必要的,主要的理由是:
   • 最大限度降低风险:如果我们知道后验概率，我们可以通过适当修改系数E[L]=∑k​∑j​∫Rj​​Lkj​p(x,Ck​)dx来简单地修改最小风险决策标准.如果我们只有判别函数，那么对损失矩阵的任何改变都需要我们重新利用训练数据解决分类问题.
   • 拒绝域:后验概率允许我们确定一个拒绝标准，将一些给出模糊结果预测数据点拒绝掉,让用户自行做出决策.
   • 类别标签先验补偿:再次考虑我们的医疗X射线问题，并假设我们从一般人群中收集了大量X射线图像用作训练数据，以便建立一个自动筛查系统.因为癌症在一般人群中很罕见，我们可能会发现，例如，每1,000个例子中只有1个对应于癌症的存在。 如果我们使用这样的数据集来训练自适应模型，由于癌症类别的比例很小，我们可能会遇到严重的困难.例如，将每个点分配给正常类的分类器已经达到99.9％的准确率，并且很难避免这种简单的解决方案.我们从每个类中选择了相同数量的例子的平衡数据集可以让我们找到更准确的模型.但是，我们必须补偿我们对训练数据的修改效果,假设我们已经使用了这样的修改数据集并找到了后验概率的模型.根据贝叶斯定理,我们看到后验概率与先验概率成正比，我们可以将其解释为每个阶段的分数分数.因此，我们可以简单地获取从我们的人工平衡数据集中获得的后验概率，并首先除以该数据集中的标签分数，然后乘以我们希望应用该模型的总体中的类别分数,最后，我们需要归一化以确保新的后验概率总和为1.请注意，如果我们直接学习判别函数而不是确定后验概率，则不能应用此方法.
   • 模型融合:对于复杂的问题，我们可能希望将问题分解为许多较小的子问题，每个子问题都可以通过一个单独的模块来解决.例如，在我们假设的医学诊断问题中，我们可能从血常规以及X射线图像中获得信息。不将所有这些异构信息组合到一个巨大的输入空间中，而是建立多个子系统协同处理一个复杂的问题可能更有效.只要两个模型中的每一个都给出了类的后验概率，我们就可以使用基于概率规则的方法组合输出.一种简单的方法是假设，对于每个类别，X射线图像的输入分布（由xI​表示）和血液数据（由x_B表示）是独立同分布的, 我们有:

   p(xI​,xB​∣Ck​)=p(x1​∣Ck​)p(xB​∣Ck​)

   这是条件独立性的应用,然后给出后验概率:

   p(Ck​∣xI​,xB​)∝p(xI​,xB​∣Ck​)p(Ck​)

   ∝p(xI​∣Ck​)p(xB​∣Ck​)p(Ck​)

   ∝p(Ck​)p(Ck​∣x1​)p(Ck​∣xB​)​

   因此，我们需要类先验概率p(Ck​)，我们可以根据每个类别中的数据点百分比估计，再将后验概率归一化，使其它们总和为1.条件独立性假设p(Ck​∣xI​,xB​)∝p(xI​,xB​∣Ck​)p(Ck​)朴素贝叶斯模型的核心思想.

回归的损失函数

到目前为止，我们已经在分类问题的背景下讨论了决策理论.我们现在转向回归问题的情况，例如前面讨论的曲线拟合示例.所谓决策阶段就是为每一个输入x给出一个估计值y(x), 假设在这样在的时候,我们会产生一个误差L(t,y(x)),然后给出预期损失:

E[L]=∫∫L(t,y(x))p(x,t)dxdt

回归问题中损失函数的一个常见选择是L(t,y(x))={y(x)−t}给出的平方损失, 在这种情况下，我们可以写出预期的损失.

E[L]=∫∫{y(x)−t}2p(x,t)dxdt

我们的目标是选择y(x)以便最小化E[L], 然后我们可以求偏导数

δy(x)δE[L]​=2∫{y(x)−t}p(x,t)dt=0

求解y(x),使用概率的求和乘积规则,我们得到

y(x)=p(x)∫tp(x,t)dt​=∫tp(t∣x)dt=Et​[t∣x]

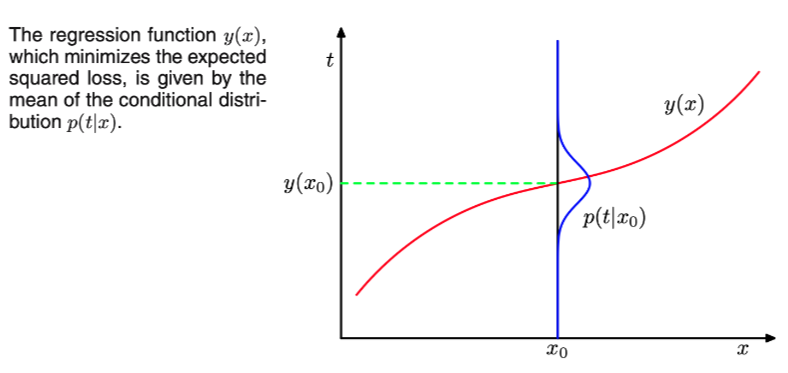
我们也可以用稍微不同的方式得出这个结果，这也将揭示回归问题的本质.有了最优解是条件期望的知识，我们可以扩展平方项如下:

{y(x)−t}2={y(x)−E[t∣x]+E[t∣x]−t}2

={y(x)−E[t∣x]}2+2{y(x)−E[t∣x]}{E[t∣x]−t}+{E[t∣x]−t}2

算法中的第一项表明了最小二乘法的最优预测值是其均值,第二项是 t 的方差.它代表了目标数据的内在可变性，可以视为噪声.事实上，我们可以确定三种不同的方法来解决回归问题，按照复杂性降低的顺序:

1. 解决联合分布p(x,t)的估计问题,然后归一化以找到条件密度p(t∣x)，最后边缘化以找到由y(x)=∫p(t∣x)dt=Et​[t∣x]给出的条件均值

2. 首先解决确定条件密度分布p(t∣x), 然后利用公式y(x)=∫p(t∣x)dt=Et​[t∣x] 边缘化给出预测结果.

3. 直接从训练数据中找到回归函数映射y(x)

这三种方法的相对优点遵循与上述分类问题相同的方法.平方损失不是回归损失函数的唯一可能选择.实际上，在某种情况下，平方损失可能导致非常差的结果，并且我们需要开发更复杂的方法.