前言
从概率论的角度看我们的目标是预测分布p(t∣x),这表达了我们对 x 的每个值对样本预测值 t 的不确定性.从这个条件分布中,我们可以对x的任何新值进行t的预测,以便最小化损失函数的期望值。尽管线性模型作为模式识别的实用技术具有显着的局限性,特别是涉及高维度输入空间的问题,但它们具有良好的分析研究的性质,并为后面章节中讨论的更复杂模型奠定了基础。
3.1 线性基函数模型
回归的最简单线性模型是涉及输入变量的线性组合的模型
y(x,w)=w0+w1x1+...+wDxD
被称为线性回归,我们注意到所谓"线性"指的是参数w是线性关系.我们认为:
y(x,w)=w0+j=1∑M−1wjϕj(x)
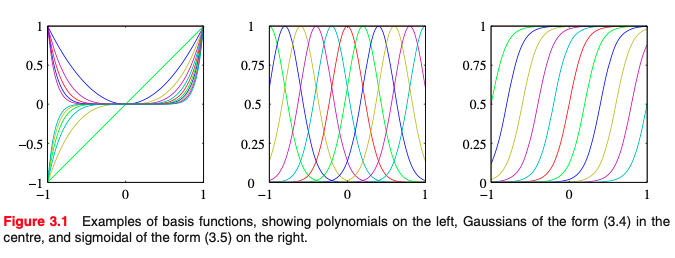
也是线性基函数, 其中ϕj(x)被称为基函数.我们允许y(x,w)是 x 的非线性函数.第1章中考虑的多项式回归的例子是该模型的一个特定例子,其中有一个输入变量x(y=w0+w1x+w2x2+w3x3), 对于基函数的选择有很多,例如:
ϕj(x)=exp{−2s2(x−uj)2}
其中μ_j控制输入空间中基函数的位置,并且参数s控制它们的空间中波动的尺度.但应注意它们不需要具有概率解释,特别是归一化系数并不重要,因为这些基函数将乘以自适应参数wj.另一种可能性是形式的Sigmoid形基函数:
ϕj(x)=σ(sx−uj)
其中σ(a)是 sigmoid 函数
σ(a)=1+exp(−a)1
极大似然与最小方差
在第1章中,我们通过最小化平方和误差函数将多项式函数拟合到数据集.我们还表明,这种误差函数可以作为假设高斯噪声模型下的最大似然解.让我们回到这个讨论,并更详细地考虑最小二乘法及其与最大似然的关系.在此之前,我们假设目标变量 t 由具有加入了高斯噪声的确定性函数 y(x,w)给出,即:
t=y(x,w)+ϵ
其中ϵ是均值为0方差为β的噪声.
p(t∣x,w,β)=N(t∣y(x,w),β(−1))
回想一下,如果我们假设一个平方损失函数,那么对于一个新的x值,最佳预测将由目标变量的条件均值给出:
E[t∣x]=∫tp(t∣x)dt=y(x,w)
注意,高斯噪声假设意味着给定x的条件分布是单峰的,这对于某些应用可能是不合适的.现在考虑一个输入数据集X={x1,...,xN}, 对应的标签为t1,...,tN假设这些数据点是独立于分布抽样的,我们得到似然函数的以下表达式,它是形式可调参数w和β的函数。
p(t∣X,w,β)=n=1∏NN(tn∣wTϕ(xn),β−1)
请注意,在监督学习问题如回归(或者分类)中,我们并不是要设计输入变量的分布模型.因此x将始终出现在条件变量集中,因此从现在开始,我们将从p(t∣x,w,β)等表达式中删除显式x,以保持符号整洁.取似然函数的对数,并利用单变量高斯的标准形式我们有
lnp(t∣w,β)=n=1∑NlnN(tn∣wTϕ(xn),β−1)
=2Nlnβ−2Nln(2π)−βED(w)
其中,平方和误差函数由定义:
ED(w)=21n=1∑N{tn−wTϕ(xn)}2
记下似然函数后,我们可以使用最大似然来确定w和β.首先考虑关于w的最大化。 正如在1.2.5节中已经讨论的那样,我们看到线性模型的条件高斯噪声分布下似然函数的最大化等效于最小化ED给出的平方和误差函数(w),对数似然函数的梯度采用形式
∇lnp(t∣w,β)=n=1∑N{tn−wTϕ(xn)}ϕ(xn)T
我们令梯度为0,则为:
0=n=1∑Ntnϕ(xn)T−wT(n=1∑Nϕ(xn)ϕ(xn)T)
对 w 求解我们可以得出:
wML=(ΦTΦ)−1ΦTt
这被称为最小二乘问题的正规方程, 其中Φ是一个N×M的矩阵,被称为设计矩阵, 设计矩阵的元素Φnj=ϕj(Xn)
统计学和机器学习中,设计矩阵(英语:design matrix)是一组观测结果中的所有解释变量的值构成的矩阵,常用X表示。设计矩阵常用于一些统计模型,如一般线性模型.y=Xβ,其中X是设计矩阵,β是对应每一种解释变量的系数组成的系数向量,y是每一个观测对应的预测值构成的向量。
Φ=⎝⎜⎜⎜⎜⎜⎜⎛ϕ0(x1)ϕ0(x2)...ϕ0(xN)ϕ1(x1)ϕ1(x2)...ϕ1(xN)ϕ2(x1)ϕ2(x2)...ϕ2(xN)............ϕM−1(x1)ϕM−2(x1)...ϕM−2(xN)⎠⎟⎟⎟⎟⎟⎟⎞
公式
Φ+≡(ΦTΦ)−1ΦT
被称为Morre-Penrose 矩阵Φ的伪逆.它可以被看作是非方阵的矩阵逆概念的推广.实际上,如果Φ是正方形和可逆的,那么使用(AB)−1=B−1A−1 我们看到Φ+≡Φ−1
在这里,我们把偏差参数w0提出来,观察偏差系数的变化情况
ED(w)=21n=1∑N{tn−w0−j=1∑M−1wjϕj(xn)}2
我们对w0求偏导,并求解w0, 我们得到:
w0=t^−j=1∑M−1wjϕj^
其中我们定义t^
t^=N1n=1∑Ntn
ϕj^=N1n=1∑Nϕj(xn)
因此,偏差w0补偿目标值平均值与基函数值的平均值加权和之间的差异.
我们还可以对噪声的大小参数β给出最大化对数似然函数:
βML1=N1n=1∑N{tn−wMLTϕ(xn)}2
我们可以看到噪声精度的倒数由回归函数周围目标值的残差给出
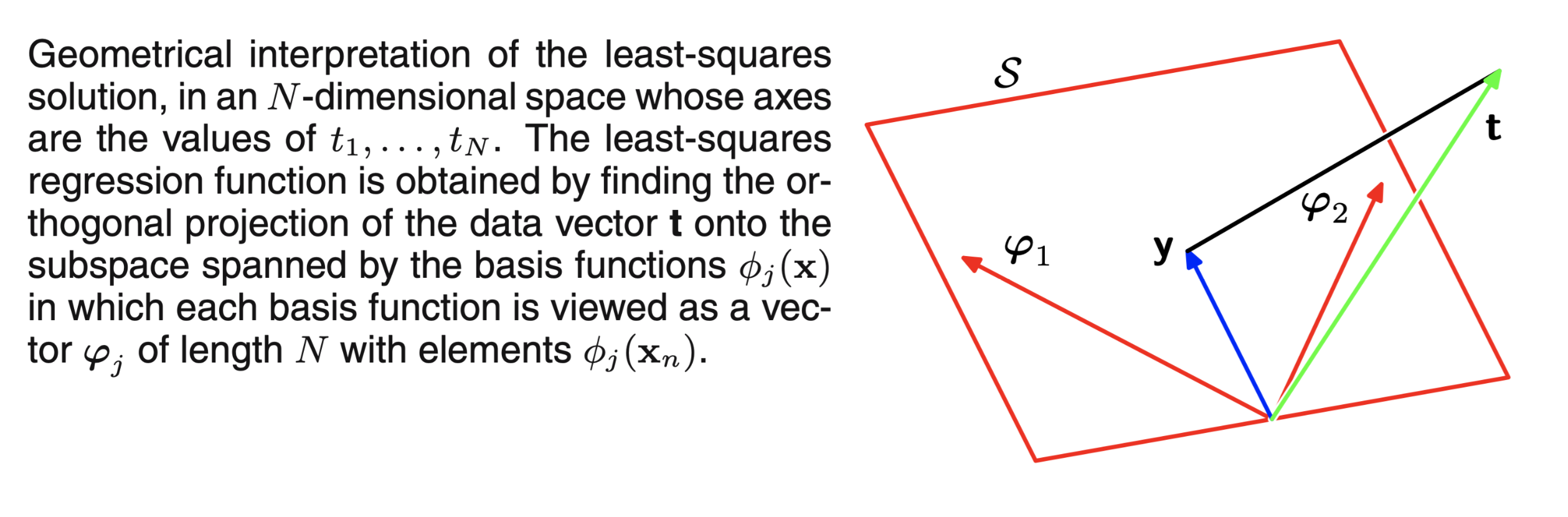
在 N 维空间中对最小二乘法的几何解释,其轴分别为t1,t2,...,tN最小二乘回归函数是找到预测数据 t 的到基函数的正交投影,其中基函数ϕj(x)可以被视为由 N 个ϕj元素组成
最小二乘法的几何解释
了解最小二乘法的几何意义解释是有必要的,对此我们考虑一个 N 维度的空间,其轴由tn给出,因此t=(t1,t2,...tN)是空间中的向量,每一个基函数ϕj(xn)在 N 个数据点预测值 t 中进行评估.其中ϕj对应于ϕ的第 j 列,而ϕ(xn)对应于Φ的第 n 行. 如果基函数的数量 M 小于数据点的数量 N,则 M 个向量ϕj(xn),则由 M 个向量构成的ϕj(xn)j将会张成一个M维度的子空间 S.因为y是矢量φj的任意线性组合,所以它可以存在于M维子空间中的任何地方.平方和误差与欧氏距离相等,因此 w 的最小二乘解对应于子空间S中最接近于 t 的 y 的选择..直观来看, 最优方案对应于t 在空间 S 上的正交投影.
在实践中,当ΦTΦ接近奇异时,正规方程的直接解可能导致数值困难.添加正则化向能够确保矩阵是非奇异的.
正则化最小均方误差
加入正则化的目的是避免过拟合,最小误差函数的形式表示如下:
ED(w)+λEw(w)
其中λ是正则化系数,λ是正则化系数,它控制数据相关误差ED(w)和正则化项EW(w)的相对重要性,正则化器的最简单形式之一是权重向量元素的平方和.
EW(w)=21wTw
如果我们也考虑由下式给出的平方和误差函数:
E(w)=21n=1∑N{tn−wTϕ(xn)}2
正则化器的这种特殊选择在机器学习文献中称为权重衰减,因为在在线学习算法中,它鼓励权重值向零衰减,除非数据支持(数据分布要求权重 w 不能为0).在统计学中,下图提供了参数收缩方法的示例,因为它将参数值缩小到0.它具有以下优点:误差函数仍然是w的二次函数,因此其精确的最小化器可以以闭合形式找到.我们对 w 求解我们得到
w=(λI+ΦTΦ)−1ΦTt
有时使用更一般的正则化器,其正则化误差采用形式.
21n=1∑N{tn−wTϕ(xn)}2+2λj=1∑M∣wj∣q
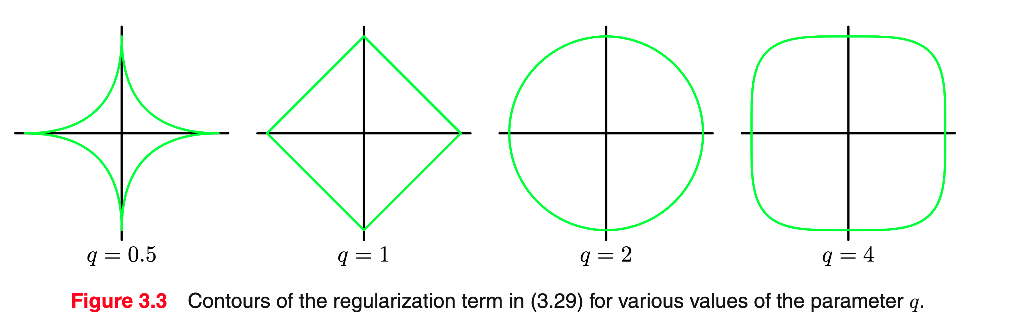
在统计学相关嗲文献中,q=1被称为 lasso.它具有如下特性:如果λ足够大,则一些系数被强制设置为零,导致稀疏模型,相应的基函数可能会不起作用.
对于η的选择,有两种方法,首先是使用拉格朗日乘子.稀疏性的起源可以从下图中看出,它显示了误差函数的最小值,受约束条件的限制,随着λ增加,因此越来越多的参数强制设置动为零.正则化允许在有限大小的数据集上训练复杂模型而不会严重过度拟合,主要是通过限制有效模型复杂性.然而,目前的问题是在模型中确定λ是一个较难的问题.
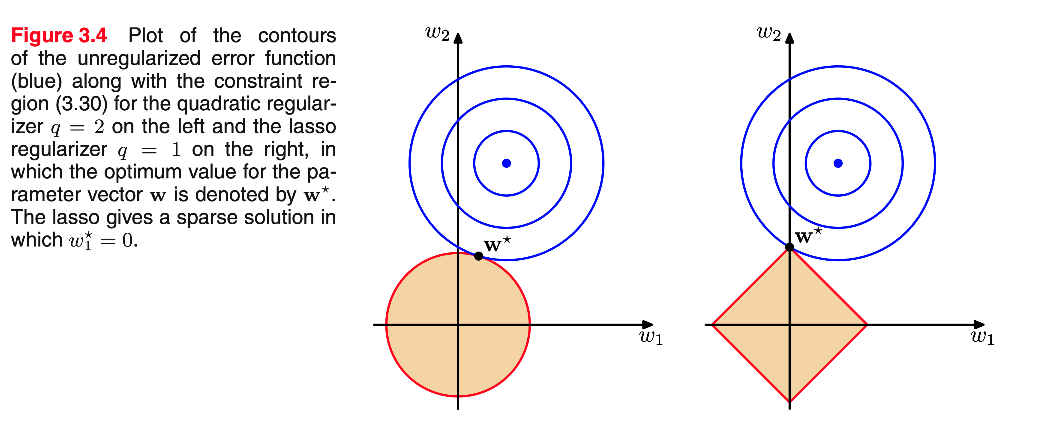
非正则误差函数的轮廓(蓝色) 其中参数矢量w的最佳值由w表示,左边为q = 2的约束区域(3.30)和右边的lasso正则化q = 1.其中参数矢量w的最佳值由w∗表示.lasso给出了一个稀疏的解决方案,其中w1∗=0
多个输出
到目前为止,我们已经考虑了单个目标变量t的情况.在一些场合中,我们可能希望预测K> 1个目标变量,我们用目标矢量t共同表示.这可以通过为t的每个分量引入一组不同的基函数来实现,从而导致多个独立的回归问题.然而,我们可以使用相同的基函数集来模拟目标向量的所有预测值,为:
y(x,w)=WTϕ(x)
其中:
y:k 维列向量
W:M×K参数矩阵
ϕ(x):由ϕj(x)组成的 M 维列向量, 其中ϕ0(x)=1
假设我们把目标向量看成高斯分布的条件概率分布, 多元高斯分布的形式为
p(t∣x,w,β)=N(t∣WTϕ(x),β−1I)
如果我们有一组数据标签t1,...,tN我们可以把它们组成一个N×K的矩阵,称为 T. 其中第 n 行的标签为tnT.类似的,我们可以把输入向量x1,...xN组成为矩阵X.然后给出对数似然函数:
lnp(T∣X,W,β)=n=1∑NlnN(tn∣WTϕ(xn),β−1I)
=2NKln(2πβ)−2βn=1∑N∣∣tn−WTϕ(xn)∣∣2
和之前一样,我们给出 W 的闭式解:
WML=(ΦTΦ)−1ΦTT
如果我们看tk的预测标签,我们有:
wk=(ΦTΦ)−1ΦTtk=Φ+tk
tk是一个 n 维的列向量,其由tnk构成,其中 n=1,...,N
因此,回归问题的解决方案是把不同目标变量之间进行分离,我们只需要计算一个伪逆矩阵(Φ+)即可.
这个结果并不令人惊讶,因为参数W只定义了高斯噪声分布的均值,我们从第2.3.4节得知多变量高斯均值的最大似然解决方案与协方差无关。多变量高斯平均值的最大似然解决方案与协方差无关。从现在开始,为简单起见,以后的章节我们只考虑单个目标变量t
f(x) tag{1.3}