一个方阵 A 是diagonalizable 当 A=PDP−1
其中 D是对角矩阵, P 是可逆矩阵
不是所有 matrix 是可以被对角化的 例如:
A=(0010)
当矩阵A 是对角化矩阵,那么有A=PDP−1
其中P=[p1,...,pn]
D=⎝⎜⎜⎜⎜⎛d1⋅⋅⋅0⋅d2⋅⋅d3⋅⋅d4⋅0⋅⋅⋅dn⎠⎟⎟⎟⎟⎞
其中矩阵pi为特征向量, D 为特征值, 我们可以说 n 个特征向量组成了一个可逆矩阵,等价于特征向量之间独立等价于n 个线性无关的特征向量可以张成一个%R^n%空间
问:如何找到对角化矩阵 A?
答:找到 n 个线性无关的特征向量组成 P,把特征值拿出来组成 D
如果特征向量刚好对应于不同的特征值(特征值不相同),我们说特征向量线性无关.
从同一个特征值下对应的不同特征向量,他们可能是线性相关的,也可能是线性无关的.

不同的特征值下的特征向量一定是线性无关的.
计算例子:
如果有三个特征值,说明该矩阵一定可以对角化,图中有两个相同的特征值,我们看他们的特征向量.

如果A=PDP−1, 那么Am=PDmP−1 应用:马尔科夫决策过程,

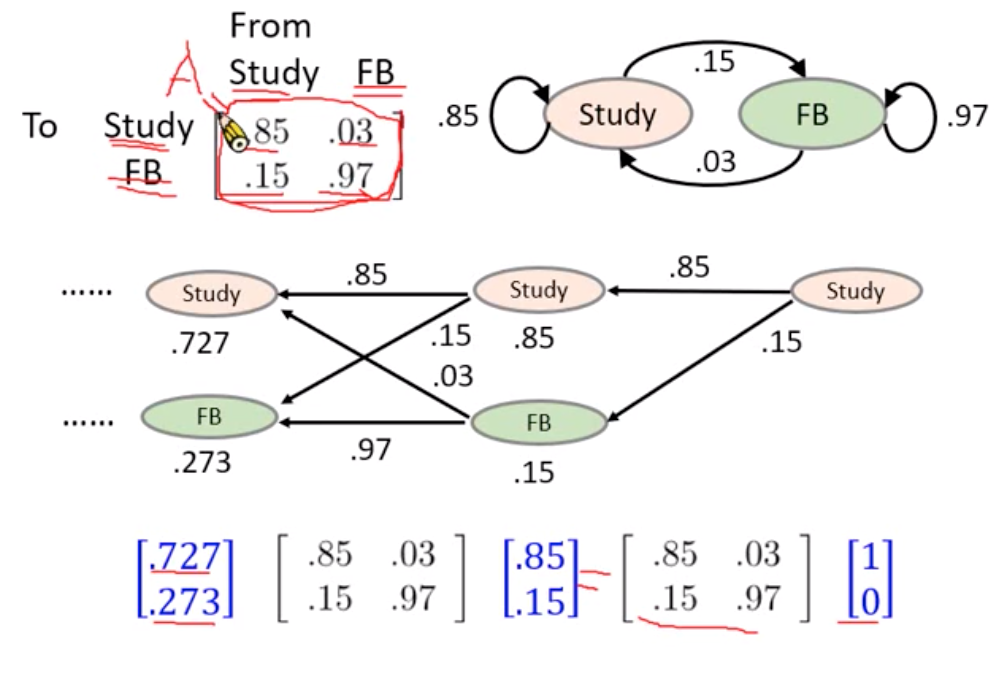
先把 A 做对角化,求特征值和特征向量

