3.2 偏差-方差分析

这章节回答了"为什么训练 loss 相同的两个模型,预测能力却完全不同"的问题.

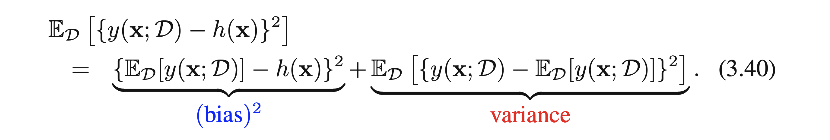
第一项称为bias 偏差，表示所有数据集的平均预测与期望的回归函数的差异程度.第二个术语，称为variance，衡量单个数据集的解决方案在其平均值附近变化的程度.

我们总结一下公式:

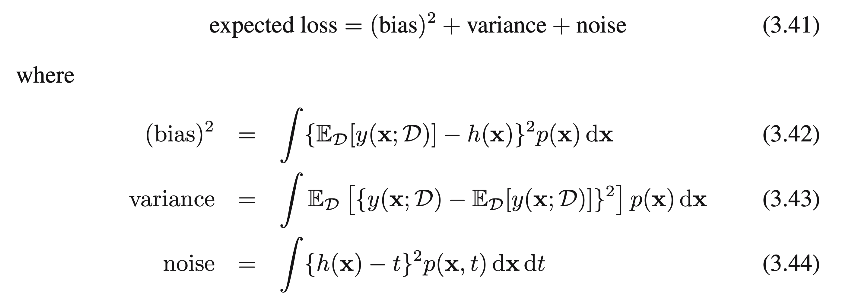
我们的目标是最小化预期损失，我们将其分解为偏差，方差和恒定噪声项的总和.我们将要看到的偏差和方差之间存在权衡，非常灵活的模型具有低偏差和高方差，相对刚性的模型具有高偏差和低方差.具有最佳预测能力的模型是导致偏差和方差之间最佳平衡的模型.(这里就解释了为什么训练 loss 相同的两个模型,预测能力却完全不同呢?)

我们接下来定量分析偏差-方差间的权衡, 我们获得所有模型的平均预测:
\hat{y}(x)=\frac1L \sum_{l=1}L y^{(l)}(x)
然后给出偏差和方差:
(bias)^2 = \frac1N \sum_{n=1}^N{\hat{y}(x_n)-h(x_n)}^2

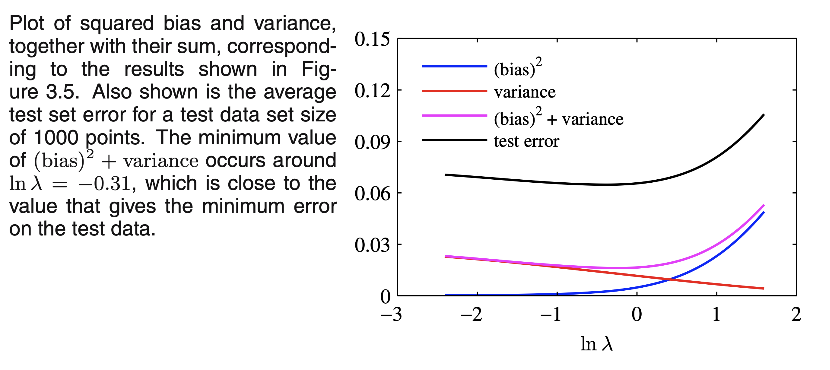
我们可以看到较小的\lambda会拉升模型的方差,但较大的lambda会拉高模型的偏差.

虽然偏差方差分解可以从频率论的角度对模型复杂性问题提供一些有趣的见解，但它使用价值不大,因为实践中我们只有一个数据集.